Matt Igel

I received an email the other day from the Zeiss Planetarium Bochum.  Staff recently celebrated the 60th anniversary of the Planetarium with a big party.  The institute’s lead artistic director baked a cake that was meant to look like something called a ‘meat hedgehog’.  It’s usually a German dish made of pork constructed to look like a hedgehog.  Because German’s love their compound words, ‘meat hedgehog’ is ‘mettigel’.  Naturally, this meant that the cake version needed a punny name.  Hence, I received the following picture from the Planetarium.

Congratulations to the Planetarium Bochum on 60 years.

By every account I’ve ever heard, Pete Rose was an absolute scoundrel.  This post isn’t about him exactly, rather it’s about different ways to success.  I previously posted about (the incomparable) Hank Aaron.  Hank was naturally skilled and hardworking, and the result was that he hit the ball very, very far.  That is usually good in baseball; hitting homeruns in a well-trodden path to success.  Hank Aaron had a career WAR of over 140.  In contrast, Pete Rose was not a natural homerun hitter nor a gifted fielder yet ended his playing career with 80 WAR.  So how did a man from the westside of Cincinnati without natural homerun skills accumulate over half of Hank Aaron’s WAR (and 10 more WAR than Derek Jeter, just saying)?  Pete Rose hit singles.  Pete Rose hit doubles.  Pete Rose hit nearly as many triples in his career and homeruns.  It’s how he earned the nickname “Charlie Hustle”.  Pete Rose put the ball in play and ran his ass off.  He figured out what he could do better than anyone else and did it.  Pete Rose’s method of success wasn’t complicated.  In many ways, it was the opposite.  And while off the field, Pete Rose was no role model, on the field, we could probably all learn a little more “hustle”.

I’m currently in the year-long process of promoting from Assistant Adjunct to Associate Adjunct.  Like my tenure-track colleagues, the process of going up for promotion has several steps.  One, is requesting external letters from faculty colleagues across the country that assess the quality of my contributions to the University’s mission.  I merely wanted to thank anyone who wrote me a letter.  It’s heartening to read frank assessments of my contributions and to see interesting anecdotes of my interactions with folks across the years.  So, thanks for taking the time to write on my behalf.

I’ve moved upstairs in Hoagland Hall to room 253.  Come check out my new digs.

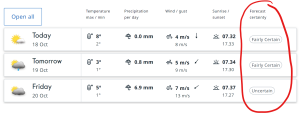
I’ve spent the last few months in Sweden.  The local official forecast entity here is the Swedish Meteorological and Hydrological Institute (SMHI).  They provide local forecasts with a dash of uncertainty thrown in.  So, in the picture below, you can see that today’s forecast is “fairly certain” while Friday’s forecast is “uncertain”.  That’s pretty cool, although even to me, it’s not entirely clear what those assessments mean despite looking around SMHI’s website for definitions.

What I think it even more fun, is a product they have rolled out in a beta form.  Below, you can see that they provide different possible forecasts.  So, rather than just providing the most likely forecast (what we might traditionally think of as the best forecast), they provide a range of reasonable forecasts.  It’s probably going to be partly cloudy today, but hey, it could be mostly cloudy, or possibly cloudy.  Regardless, it’ll probably be ~7C.  Tomorrow is more interesting.  It will most likely rain, but the second most likely forecast is sunny.  Without this kind of categorical forecast, we might be tempted to split the difference and provide some kind of intermediate precipitation probability and cloud cover.  But doing so risks misrepresenting the forecast.  Maybe the possible futures are 1) 100% cloud cover and extensive rain or 2) clear skies.  Providing a forecast that weights by the probability of those outcomes might be A) 75% cloud cover and intermittent rain.  But that’s not really a likely future because it’s not 1) or 2) so it’s wrong from the star

Warning: this post has no real point!

We’re almost done with another quarter, and it’s been one I never anticipated.  I’ve been here in Davis since 2016.  In that time, I’ve done a lot of things I never expected to do in this adjunct position.  I’ve given a lot of interesting media interviews.  I’ve gotten to go all sorts of interesting places.  I’ve gotten to work with lots of interesting and clever students.  And, I have taught a lot more than I ever expected.  It’s a fun job.  But, it’s a job that doesn’t come with enough hours in any given week to do everything that needs to be done.  Teaching essentially full time this quarter has been good in some senses because I can compartmentalize.  I hope students have learned something useful and that I haven’t led them too far astray.  If nothing else, I’ve had fun.  If I owe you an email response, it’s coming in June.

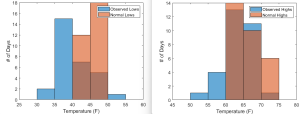
Yep, November was reasonably cool in the Sacramento area.  This was felt mostly in the lows.  The median low temperature for the month was 39F while the normal median is 45F.  The median high temperature was 1 degree below the normal median of 65F.   Below are the distributions of November 2022 lows and highs.  Despite the cool weather, we never even came close to setting a record low in Sacramento*, but it is quite possible that the high temperature on the 8th of just 53F was at least within sight of the record-low high-temperature for the day.

*The official low this morning in Davis of 30F would tie the official low in Sacramento for this date.  The low at Travis AFB was 26F!

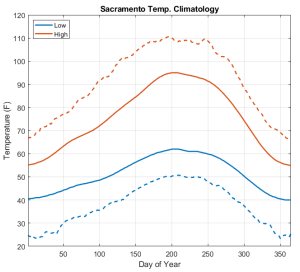
So, I want to talk a little bit about Sacramento temperature climatology.  This first figure below is what you might expect to see when thinking about temperature statistics: “normal” lows and highs; and “record” lows and highs.  These will feel familiar to anyone who lives in the Central Valley.  We have mild winters with little diurnal range and rather warm record lows.  We have what you might consider a long spring with slowly increasing normal highs and lows.  We have a very hot summer followed by quickly cooling normal and record temperatures in fall.  What I’m showing below is actually the 10-day running mean of temperatures.  This helps smooth out all the bumps and wiggles in the data.

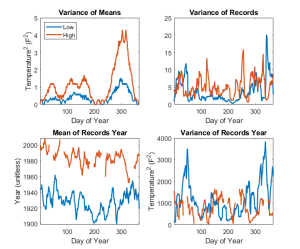
But, what I really want to talk about is the variance of the normal and record temperatures.  Below, I’ve included a figure with 4 panels.  The first is the 10-day running variance (or variability) of the normal temperatures.  Since normals are locally monotonic (in time), this panel shows us how quickly the normal high and low change.  As we might have inferred from above, normal highs vary at 10-day time scales more than normal lows and do so most strongly toward the end of the year.  Interestingly, the second panel (the 10-day variance of the records) doesn’t look at all like the first panel.  The variance in record high temperatures is wiggly but functionally constant across the year.  This is not what I expected.  I had imagined the record highs would vary strongly in the summer and weakly in the winter.  The variance of the record low peaks in the cold season and is near zero around day 225 (mid-August).

On the bottom row, I have plotted 1) the 10-day running mean of the year of the record high and low (gaps occur when the same record is set in multiple years) and 2) the 10-day variance of the year of records.  Here, we see an obvious global warming signal — much more recent mean years of high temperature records than low.  The average difference is 56 years!  That’s incredible.  Also noteworthy: the 10-day mean year of record high decreases throughout the year.  I have no idea what to make of that — Our winters are more record warm than our falls?  The 10-day variance of the year of records is also a bit surprising.  Here, we see peaks in record low occurrence year in the cold season.  It seems (from this figure and looking at the raw data) that in the winter, we’ve actually had lots of instances of contemporary record lows even if on average they primarily occurred prior to 1940.

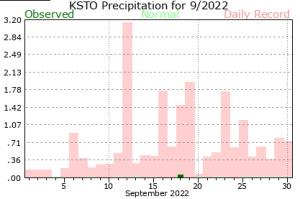
24 hour accumulation of precipitation to 7am on the 19th in Davis was about 1″.  Below is the record (for Sacramento, at least) daily rainfall values for the month of September.  A 1″ storm would easily be a top 10 daily accumulation.  So, this rain was in rare company but was hardly unprecedented.

Records for the 23rd, 24th, and 25th were all set in 1904.  Assuming that was just one storm, total rainfall from that single event was (at least) 3.50″!

The group is excited to announce new funding from the National Science Foundation to help us better understand the dynamics of convective circulations.